Contents   Index

Parallelepiped periodic boundaries (IMCON=3)

 

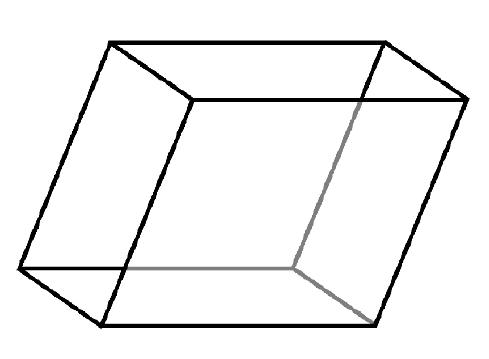
The parallelepiped MD cell.

The parallelepiped (e.g. monoclinic or triclinic) cell is generally used in simulations of crystalline materials, where its shape and dimension is commensurate with the unit cell of the crystal. Thus for a unit cell specified by three principal vectors $\mbox{$\underline{a}$}$, $\mbox{$\underline{b}$}$, $\mbox{$\underline{c}$}$, the MD cell is defined in the DL_POLY_2 CONFIG file by the vectors (L$a_{1}$,L$a_{2}$,L$a_{3}$), (M$b_{1}$,M$b_{2}$,M$b_{3}$), (N$c_{1}$,M$c_{2}$,N$c_{3}$), in which L,M,N are integers, reflecting the multiplication of the unit cell in each principal direction. Note that the atomic coordinate origin is the centre of the MD cell.

The parallelepiped boundary condition can be used with the Ewald summation method.