![]()
f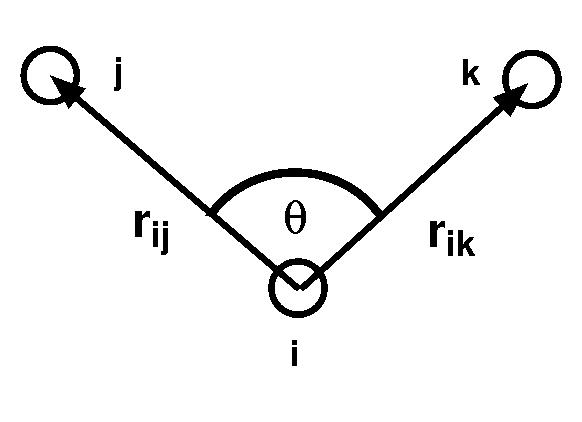
The valence angle and associated vectors
The valence angle potentials describe the bond bending terms between the specified atoms. They should not be confused with the three body potentials described later, which are defined by atom types rather than indices.
| (2.12) |
| (2.13) |
| (2.14) |
| (2.15) |
![$\displaystyle {k \over 8(\theta_{jik}-\pi)^2}\left\{ \left[
(\theta_0 -\pi)^2 -(\theta_{jik}-\pi)^2\right]^2
\right\}$](img103.png) |
|||
| (2.16) |
| (2.17) |
| (2.18) |
| (2.19) |
In these formulae ![]() is the angle between bond vectors
is the angle between bond vectors ![]() and
and ![]() :
:
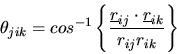 |
(2.20) |
In DL_POLY_2 the most general form for the valence angle potentials
can be written as:
| (2.21) |
where ![]() is a purely angular function and
is a purely angular function and ![]() is a screening or truncation
function. All the function arguments are scalars. With this reduction the force on an atom
derived from the valence angle potential is given by:
is a screening or truncation
function. All the function arguments are scalars. With this reduction the force on an atom
derived from the valence angle potential is given by:
| (2.22) |
with atomic label ![]() being one of
being one of ![]() and
and ![]() indicating the
indicating the ![]() component. The derivative is
component. The derivative is
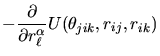 |
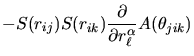 |
||
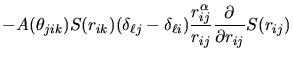 |
|||
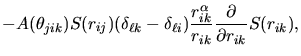 |
(2.23) |
with ![]() if
if ![]() and
and ![]() if
if ![]() . In the absence of screening terms
. In the absence of screening terms ![]() , this
formula reduces to:
, this
formula reduces to:
| (2.24) |
The derivative of the angular function is
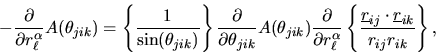 |
(2.25) |
with
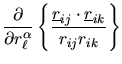 |
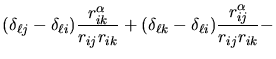 |
||
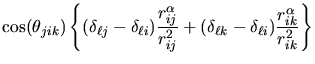 |
(2.26) |
The atomic forces are then completely specified by the derivatives of the particular
functions ![]() and
and ![]() .
.
The contribution to be added to the atomic virial is given by
| (2.27) |
It is worth noting that in the absence of screening terms S(r), the virial is zero [26].
The contribution to be added to the atomic stress tensor is given by
| (2.28) |
and the stress tensor is symmetric.
In DL_POLY_2 valence forces are handled by the routine ANGFRC.
![]()