c CCLRC
Section 3.2
3.2
Bond Constraints
The SHAKE algorithm for bond constraints was devised by Ryckaert et al. [
in molecular simulation. It is a two stage algorithm based on the leapfrog Verlet integration scheme
[
]. In the first stage the LFV algorithm calculates the motion of the atoms in the system assuming
a complete absence of the rigid bond forces. The positions of the atoms at the end of this stage do
not conserve the distance constraint required by the rigid bond and a correction is necessary. In the
second stage the deviation in the length of a given rigid bond is used retrospectively to compute
the constraint force needed to conserve the bondlength. It is relatively simple to show that the
constraint force has the form
G
ij
1
2
µ
ij
t
2
(d
2
ij
- d
2
ij
)
d
o
ij
· d
ij
d
o
ij
,
(3.13)
where: µ
ij
is the reduced mass of the two atoms connected by the bond; d
o
ij
and d
ij
are the original
and intermediate bond vectors; d
ij
is the constrained bondlength; and t is the Verlet integration
time step. It should be noted that this formula is an approximation only.
The RATTLE algorithm was devised by Andersen [
] and it fits within the concept of the Velocity
Verlet integration scheme. It consists of two parts RATTLE VV1 and RATTLE VV2 applied
respectively in stages one and two of Velocity Verlet algorithm. RATTLE VV1 is similar to the
SHAKE algorithm as described above and handles the bond length constraint. However, due to
the difference in the velocity update between VV (VV1) and LFV schemes, the constraint force
generated to conserve the bondlength in RATTLE VV1 has the form as in (
factor of a half:
G
ij
µ
ij
t
2
(d
2
ij
- d
2
ij
)
d
o
ij
· d
ij
d
o
ij
.
(3.14)
The constraint force in RATTLE VV2 imposes a new condition of rigidity on constraint bonded
atom velocities.
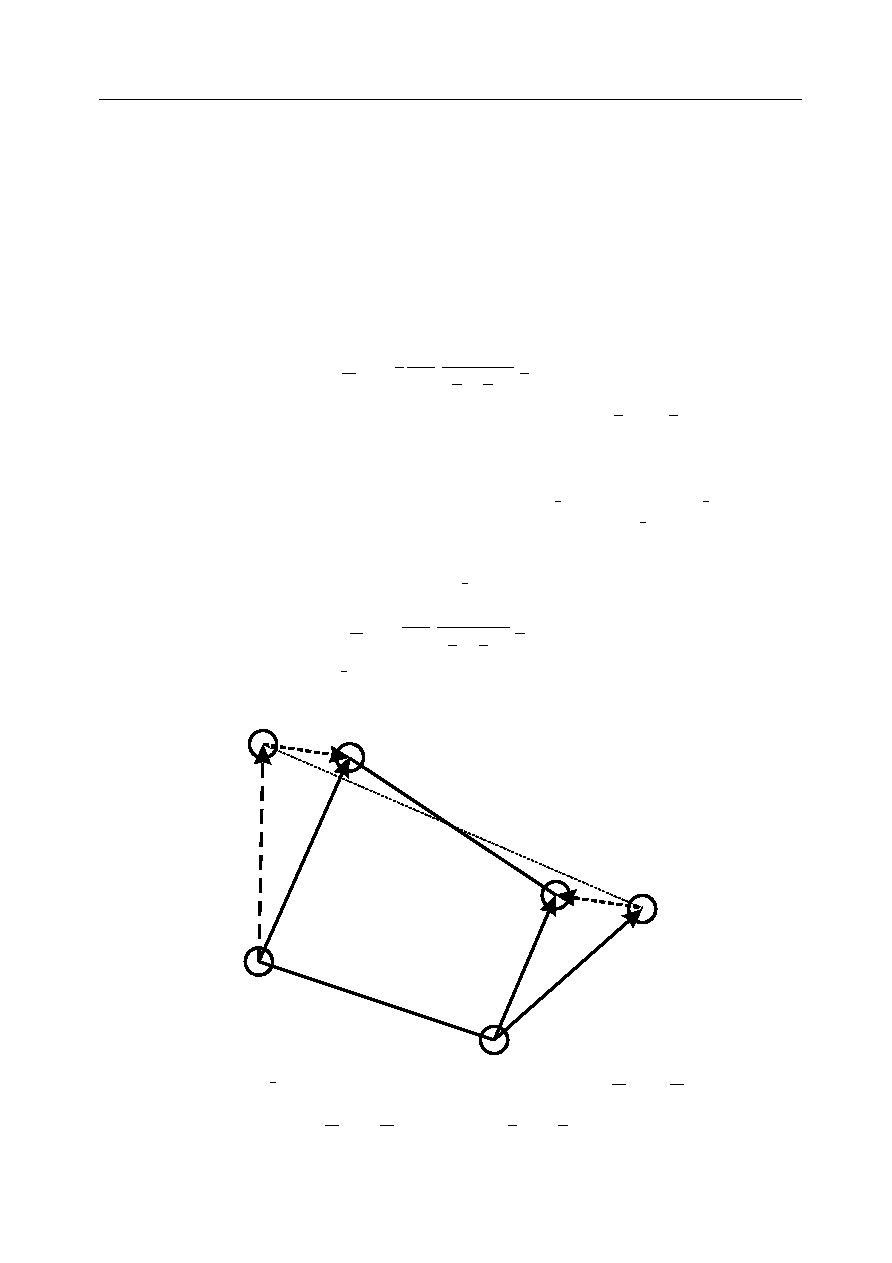
i
j
d
ij
o
d
ij
i
j
j'
i'
G
ji
G
ij
d'
ij
The SHAKE (RATTLE VV1) algorithm calculates the constraint force G
ij
= -G
ji
that conserves
the bondlength d
ij
between atoms i and j, following the initial movement to positions i and j
under the unconstrained forces F
i
and F
j
and velocities v
i
and v
j
.
45
