which can be any character string up to 80 characters in length. (Note: this is not a directive, just a simple character string.)
where n is the number of times a molecule of this type appears in the simulated system. The molecular data then follow in subsequent records:
where n indicates the number of atoms in this type of molecule. A number of records follow, each giving details of the atoms in the molecule i.e. site names, masses and charges. Each record carries the entries:
sitnam a8 atomic site nameThe integer nrept need not be specified (in which case a value of 1 is assumed.) A number greater than 1 specified here indicates that the next (nrept - 1) entries in the CONFIG file are ascribed the atomic characteristics given in the current record. The sum of the repeat numbers for all atoms in a molecule should equal the number specified by the atoms directive.
weight real atomic site mass
chge real atomic site charge
nrept integer repeat counter
ifrz integer `frozen' atom (if ifrz)
igrp integer neutral/charge group number
where n is the number of core-shell units. Each of the subsequent n records contains:
index 1 integer site index of coreThe spring force constant is entered in units of engunit Å
index 2 integer site index of shell
spring real force constant of core-shell spring
Note that the atomic site indices referred to in this table are indices arising from numbering each atom in the molecule from 1 to the number specified in the atoms directive for this molecule. This same numbering scheme should be used for all descriptions of this molecule, including the bonds, constraints, angles, and dihedrals entries described below. DL_POLY_2 will itself construct the global indices for all atoms in the systems.
This directive (and associated data records) need not be specified if the molecule contains no core-shell units.
where n is the number of flexible chemical bonds in the molecule. Each of the subsequent n records contains:
bond key a4 see table 4.7The meaning of these variables is given in table 4.7. This directive (and associated data records) need not be specified if the molecule contains no flexible chemical bonds. See the note on the atomic indices appearing under the shell directive above.
index 1 integer first atomic site in bond
index 2 integer second atomic site in bond
variable 1 real potential parameter see table 4.7
variable 2 real potential parameter see table 4.7
variable 3 real potential parameter see table 4.7
variable 4 real potential parameter see table 4.7
| key | potential type | Variables (1-4) | functional form | |||
| harm | Harmonic |
|
||||
| -hrm | ||||||
| mors | Morse |
|
||||
| -mrs | ||||||
| 12-6 | 12-6 |
|
||||
| -126 | ||||||
| rhrm | Restraint |
|
||||
|
|
||||||
| -rhm | ||||||
| quar | Quartic |
|
||||
| -qur | ||||||
Note: bond potentials with a dash (-) as the first character of the keyword, do not contribute to the excluded atoms list (see section 2.1). In this case DL_POLY_2 will also calculate the nonbonded pair potentials between the described atoms, unless these are deactivated by another potential specification.
where n is the number of constraint bonds in the molecule. Each of the following n records contains:
index 1 integer first atomic indexThis directive (and associated data records) need not be specified if the molecule contains no constraint bonds. See the note on the atomic indices appearing under the shell directive above.
index 2 integer second atomic index
bondlength real constraint bond length
where b is the potential of mean force bondlength (Å). There follows the definitions of two PMF units:
- pmf unit n
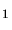
where n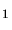 is the number of sites in the first unit. The
subsequent n
is the number of sites in the first unit. The
subsequent n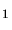 records provide the site indices and weighting.
Each record contains:
records provide the site indices and weighting.
Each record contains:
index integer atomic site index
weight real site weighting
- pmf unit n
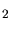
where n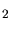 is the number of sites in the second unit. The
subsequent n
is the number of sites in the second unit. The
subsequent n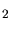 records provide the site indices and weighting.
Each record contains:
records provide the site indices and weighting.
Each record contains:
index integer atomic site index
weight real site weighting
where
Note that the directive ensemble pmf must be specified in the CONTROL file for this option to be implemented correctly.
where n is the number of valence angle bonds in the molecule. Each of the n records following contains:
| key | potential type | Variables (1-4) | functional form |
|||
| harm | Harmonic |
|
||||
| -hrm | ||||||
| quar | Quartic |
|
||||
| -qur | ||||||
| thrm | Truncated harmonic |
|
||||
| -thm | ||||||
| shrm | Screened harmonic |
|
||||
| -shm | ||||||
| bvs1 | Screened Vessal[24] |
|
||||
| -bv1 |
|
|||||
| bvs2 | Truncated Vessal[25] |
|
||||
| -bv2 |
|
|||||
| hcos | Harmonic Cosine |
|
||||
| -hcs | ||||||
| cos | Cosine |
|
||||
| -cos | ||||||
Note: valence angle potentials with a dash (-) as the first character of the keyword, do not contribute to the excluded atoms list (see section 2.1). In this case DL_POLY_2 will calculate the nonbonded pair potentials between the described atoms.
angle key a4 potential key. See table 4.8The meaning of these variables is given in table 4.8. See the note on the atomic indices appearing under the shell directive above. This directive (and associated data records) need not be specified if the molecule contains no angular terms.
index 1 integer first atomic index
index 2 integer second atomic index (central site)
index 3 integer third atomic index
variable 1 real potential parameter see table4.8
variable 2 real potential parameter see table4.8
where n is the number of dihedral interactions present in the molecule. Each of the following n records contains:
dihedral key a4 potential key. See table 4.9The meaning of the variables 1-3 is given in table 4.9. The variables 4 and 5 specify the scaling factor for the 1-4 electrostatic and Van der Waals nonbonded interactions respectively. This directive (and associated data records) need not be specified if the molecule contains no dihedral angle terms. See the note on the atomic indices appearing under the shell directive above.
index 1 integer first atomic index
index 2 integer second atomic index
index 3 integer third atomic index
index 4 integer fourth atomic index
variable 1 real potential parameter see table4.9
variable 2 real potential parameter see table4.9
variable 3 real potential parameter see table4.9
variable 4 real 1-4 electrostatic interaction scale factor.
variable 5 real 1-4 Van der Waals interaction scale factor.
| key | potential type | Variables (1-3) | functional form |
||
| cos | Cosine |
|
|||
| harm | Harmonic |
|
|||
| hcos | Harmonic cosine |
|
|||
| cos3 | Triple cosine |
|
|||
|
|
|||||
where n is the number of inversion interactions present in the molecule. Each of the following n records contains:
inversion key a4 potential key. See table 4.10The meaning of the variables 1-2 is given in table 4.10. This directive (and associated data records) need not be specified if the molecule contains no inversion angle terms. See the note on the atomic indices appearing under the shell directive above.
index 1 integer first atomic index
index 2 integer second atomic index
index 3 integer third atomic index
index 4 integer fourth atomic index
variable 1 real potential parameter see table4.10
variable 2 real potential parameter see table4.10
| key | potential type | Variables (1-2) | functional form |
|
| harm | Harmonic |
|
||
| hcos | Harmonic cosine |
|
||
| plan | Planar |
|
||
where n is the number of rigid units in the molecule. It is followed by at least n records, each specifying the sites in a rigid unit:
m integer number of sites in rigid unitUp to 15 sites can be specified on the first record. Additional records are used if necessary. Up to 16 sites are specified per record thereafter.
site 1 integer first site atomic index
site 2 integer second site atomic index
site 3 integer third site atomic index
.. .. etc.
site m integer m'th site atomic index
This directive (and associated data records) need not be specified if the molecule contains no rigid units. See the note on the atomic indices appearing under the shell directive above.
where n is the number of tethered atoms in the molecule. It is followed by n records specifying the tethered sites in the molecule:
tether key a4 tethering potential key see table 4.11This directive (and associated data records) need not be specified if the molecule contains no tethered atoms. See the note on the atomic indices appearing under the shell directive above.
index integer atomic index
variable 1 real potential parameter see table4.11
variable 2 real potential parameter see table4.11
variable 3 real potential parameter see table4.11
variable 4 real potential parameter see table4.11
| key | potential type | Variables (1-3) | functional form | ||
| harm | Harmonic |
|
|||
| rhrm | Restraint |
|
|||
|
|
|||||
| quar | Quartic |
|
|||
This directive is entered to signal to DL_POLY_2 that the entry of the details of a molecule has been completed.
The entries for a second molecule may now be entered, beginning with the name-of-molecule record and ending with the finish directive.
The cycle is repeated until all the types of molecules indicated by the molecules directive have been entered.