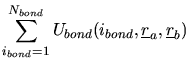 |
|||
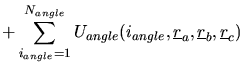 |
|||
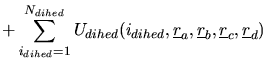 |
|||
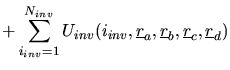 |
|||
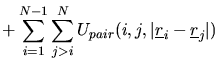 |
|||
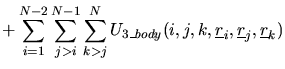 |
|||
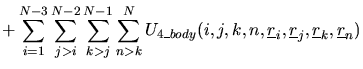 |
|||
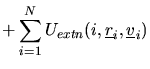 |
(2.1) |
The force field is the set of functions needed to define the interactions in a molecular system. These may have a wide variety of analytical forms, with some basis in chemical physics, which must be parameterised to give the correct energy and forces. A huge variety of forms is possible and for this reason the DL_POLY_2 force field is designed to be adaptable. While it is not supplied with its own force field parameters, many of the functions familiar to GROMOS, [3] Dreiding [8] and AMBER [4] users have been coded in the package, as well as less familiar forms. In addition DL_POLY_2 retains the possibility of the user defining additional potentials.
In DL_POLY_2 the total configuration energy of a molecular system may
be written as:
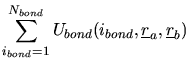 |
|||
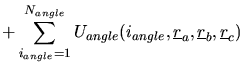 |
|||
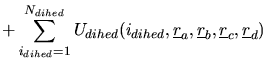 |
|||
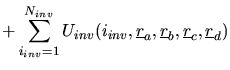 |
|||
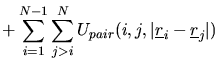 |
|||
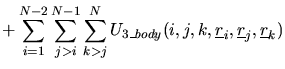 |
|||
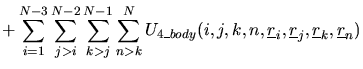 |
|||
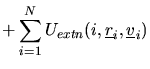 |
(2.1) |
The indices ![]() ,
, ![]() (and
(and ![]() ,
, ![]() ) appearing in the pair-body (and
three or four-body) terms indicate the atoms involved in the interaction.
There is normally a very large number of these and they are therefore
specified according to atom types rather than indices. In
DL_POLY_2 it is assumed that the pair-body terms arise from van der
Waals
and/or electrostatic (Coulombic) forces. The former are regarded as
short ranged interactions and the latter as long ranged. Long range
forces require special techniques to evaluate accurately (see section
2.4.) In DL_POLY_2 the three-body terms are restricted to valence
angle and H-bond forms. The nonbonded, three-body and four-body
interactions are globally specified according to the types of
atoms involved. DL_POLY_2 also has the ability to handle metals via density
dependent functions (see below). Though essentially many-body
potentials they are handled in DL_POLY_2 as special forms of pair potential.
) appearing in the pair-body (and
three or four-body) terms indicate the atoms involved in the interaction.
There is normally a very large number of these and they are therefore
specified according to atom types rather than indices. In
DL_POLY_2 it is assumed that the pair-body terms arise from van der
Waals
and/or electrostatic (Coulombic) forces. The former are regarded as
short ranged interactions and the latter as long ranged. Long range
forces require special techniques to evaluate accurately (see section
2.4.) In DL_POLY_2 the three-body terms are restricted to valence
angle and H-bond forms. The nonbonded, three-body and four-body
interactions are globally specified according to the types of
atoms involved. DL_POLY_2 also has the ability to handle metals via density
dependent functions (see below). Though essentially many-body
potentials they are handled in DL_POLY_2 as special forms of pair potential.
In DL_POLY_2 the intramolecular bonded terms are handled using bookkeeping arrays, which specify the atoms involved in a particular interaction and point to the appropriate arrays of parameters that define the potential. The calculation of bonded forces therefore follows the simple scheme:
DL_POLY_2 calculates the nonbonded pair interactions using a
Verlet neighbour list [12] which is reconstructed at
intervals during the simulation. This list records the indices of all
`secondary' atoms within a certain radius of each `primary' atom; the
radius being the cut-off radius (![]() ) normally applied to the
nonbonded potential function, plus an additional increment (
) normally applied to the
nonbonded potential function, plus an additional increment (
![]() ). The neighbour list removes the need to scan over all atoms
in the simulation at every timestep. The larger radius
(
). The neighbour list removes the need to scan over all atoms
in the simulation at every timestep. The larger radius
(
![]() ) means the same list can be used for several
timesteps without requiring an update. The frequency at which the list
must be updated depends on the thickness of the region
) means the same list can be used for several
timesteps without requiring an update. The frequency at which the list
must be updated depends on the thickness of the region
![]() . DL_POLY_2 has two methods for constructing the neighbour
list: the first is based on the Brode-Ahlrichs scheme
[22] and is used when
. DL_POLY_2 has two methods for constructing the neighbour
list: the first is based on the Brode-Ahlrichs scheme
[22] and is used when ![]() is large in comparison with
the simulation cell; the second uses the link-cell algorithm
[23] when
is large in comparison with
the simulation cell; the second uses the link-cell algorithm
[23] when ![]() is relatively small. The potential
energy and forces arising from the nonbonded interactions are
calculated using interpolation tables.
is relatively small. The potential
energy and forces arising from the nonbonded interactions are
calculated using interpolation tables.
A complication in the construction of the Verlet neighbour list for macromolecules is the concept of excluded atoms, which arises from the need to exclude certain atom pairs from the overall list. Which atom pairs need to be excluded is dependent on the precise nature of the force field model, but as a minimum atom pairs linked via extensible bonds or constraints and atoms (grouped in pairs) linked via valence angles are probable candidates. The assumption behind this requirement is that atoms that are formally bonded in a chemical sense, should not participate in nonbonded interactions. (However this is not a universal requirement of all force fields.) The same considerations are needed in dealing with charged excluded atoms. DL_POLY_2 has several subroutines available for constructing the Verlet neighbour list, while taking care of the excluded atoms (see chapters 3 and 8 for further information.)
Three- and four-body nonbonded forces are assumed to be short ranged and therefore calculated using the link-cell algorithm [23]. They ignore the possibility of there being any excluded interactions involving the atoms concerned.
Throughout this section the description of the force field assumes the simulated system is described as an assembly of atoms. This is for convenience only and readers should understand that DL_POLY_2 does recognise molecular entities, defined either through constraint bonds or rigid bodies. In the case of rigid bodies, the atomic forces are resolved into molecular forces and torques. These matters are discussed in greater detail later in sections 2.5.1 and 2.5.6).
Note that the subroutines mentioned in the subsections of this chapter are described in greater detail in chapter 8 of the Reference Manual.