Contents   Index

Bond Constraints

The SHAKE algorithm for bond constraints was devised by Ryckaert et al. [13] and is widely used in molecular simulation. It is a two stage algorithm based on the Verlet integration scheme [12]. DL_POLY_2 employs a leapfrog variant. In the first stage the Verlet leapfrog algorithm calculates the motion of the atoms in the system assuming a complete absence of the rigid bond forces. The positions of the atoms at the end of this stage do not conserve the distance constraint required by the rigid bond and a correction is necessary. In the second stage the deviation in the length of a given rigid bond is used retrospectively to compute the constraint force needed to conserve the bondlength. It is relatively simple to show that the constraint force has the form

$$\mbox{$\underline{G}$}_{ij}\approx\frac{\mu_{ij}(d_{ij}^{2}-... ...ot\mbox{$\underline{d}$}_{ij}'}\mbox{$\underline{d}$}_{ij}^{o}$$ (2.178)

where: $\mu_{ij}$ is the reduced mass of the two atoms connected by the bond;  $\mbox{$\underline{d}$}_{ij}^{o}$ and $\mbox{$\underline{d}$}_{ij}'$ are the original and intermediate bond vectors; $d_{ij}$ is the constrained bondlength; and $\Delta t$ is the Verlet integration time step. It should be noted that this formula is an approximation only.

 

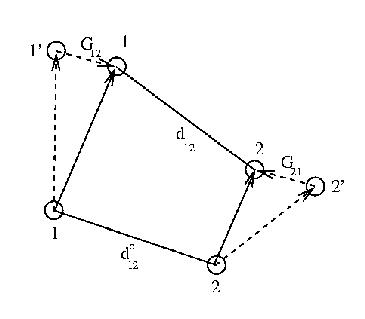
The SHAKE algorithm calculates the constraint force $\mbox{$\underline{G}$}_{12}=-\mbox{$\underline{G}$}_{21}$ that conserves the bondlength $d_{12}$ between atoms $1$ and $2$, following the initial movement to positions $1'$ and $2'$ under the unconstrained forces $\mbox{$\underline{F}$}_{1}$ and $\mbox{$\underline{F}$}_{2}$.

 

For a system of simple diatomic molecules, computation of the constraint force will, in principle, allow the correct atomic positions to be calculated in one pass. However in the general polyatomic case this correction is merely an interim adjustment, not only because the above formula is approximate, but the successive correction of other bonds in a molecule has the effect of perturbing previously corrected bonds. The SHAKE algorithm is therfore iterative, with the correction cycle being repeated for all bonds until each has converged to the correct length, within a given tolerance. The tolerance may be of the order $10^{-4}~\AA$ to $10^{-8}~\AA$ depending on the precision desired.

The procedure may be summarised as follows:

1. All atoms in the system are moved using the Verlet algorithm, assuming an absence of rigid bonds (constraint forces). (This is stage 1 of the SHAKE algorithm.)
2. The deviation in each bondlength is used to calculate the corresponding constraint force (2.178) that (retrospectively) `corrects' the bond length.
3. After the correction (2.178) has been applied to all bonds, every bondlength is checked. If the largest deviation found exceeds the desired tolerance, the correction calculation is repeated.
4. Steps 2 and 3 are repeated until all bondlengths satisfy the convergence criterion (This iteration constitutes stage 2 of the SHAKE algorithm).

The parallel version of this algorithm, as implemented in DL_POLY_2 , is known as RD_SHAKE [11] (see section 2.6.8). The subroutine NVE_1 implements the Verlet leapfrog algorithm with bond constraints. The routine RDSHAKE_1 is called to apply the SHAKE corrections to position.

It should be noted that the fully converged constraint forces $G_{ij}$ make a contribution to the system virial and the stress tensor.

The contribution to be added to the atomic virial (for each constrained bond) is

$${\cal W}=-\mbox{$\underline{d}$}_{ij}\cdot\mbox{$\underline{G}$}_{ij}.$$ (2.179)

The contribution to be added to the atomic stress tensor is given by

$$\sigma^{\alpha \beta}=d_{ij}^{\alpha}G_{ij}^{\beta},$$ (2.180)

where $\alpha$ and $\beta$ indicate the $x,y,z$ components. The atomic stress tensor derived from the pair forces is symmetric.

  Contents   Index