![]()
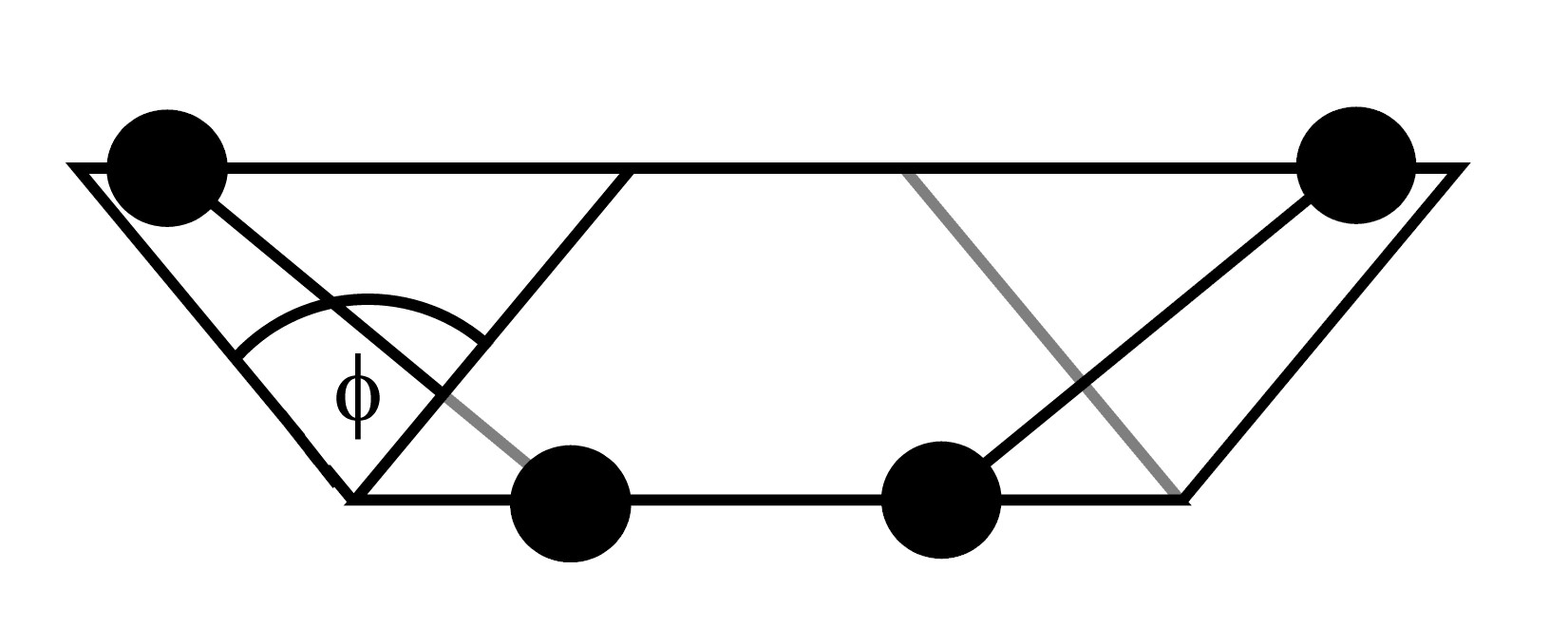
The dihedral angle and associated vectors
The dihedral angle potentials describe the interaction arising from torsional forces in molecules. (They are sometimes referred to as torsion potentials.) They require the specification of four atomic positions. The potential functions available in DL_POLY_2 are as follows.
| (2.29) |
| (2.30) |
| (2.31) |
| (2.32) |
In these formulae ![]() is the dihedral angle defined by
is the dihedral angle defined by
| (2.33) |
with
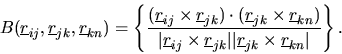 |
(2.34) |
With this definition, the sign of the dihedral angle is positive if
the vector product ![]() is in the same direction as the bond vector
is in the same direction as the bond vector ![]() and negative if in the opposite direction.
and negative if in the opposite direction.
The force on an atom arising from the dihedral potential is given by
| (2.35) |
with ![]() being one of
being one of ![]() and
and ![]() one of
one of ![]() . This may be expanded into
. This may be expanded into
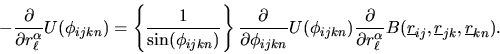 |
(2.36) |
The derivative of the function ![]() is
is
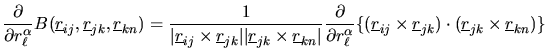 |
(2.37) | ||
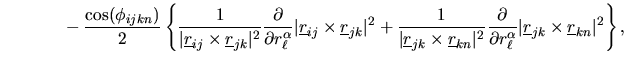 |
with
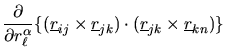 |
|||
| (2.38) |
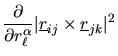 |
|||
| (2.39) |
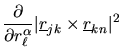 |
|||
| (2.40) |
Where we have used the the following definition:
![\begin{displaymath}[\mbox{$\underline{a}$} ~
\mbox{$\underline{b}$}]_{\alpha}=\sum_{\beta}(1-\delta_{\alpha\beta})a^{\beta}b^{\beta}.
\end{displaymath}](img161.png) |
(2.41) |
Formally, the contribution to be added to the atomic virial is given by
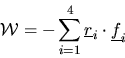 |
(2.42) |
However it is possible to show (by tedious algebra using the above formulae, or more elegantly by thermodynamic arguments [26],) that the dihedral makes no contribution to the atomic virial.
The contribution to be added to the atomic stress tensor is given by
| (2.43) | |||
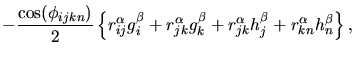 |
with
| (2.44) | |||
| (2.45) | |||
| (2.46) | |||
| (2.47) | |||
| (2.48) | |||
| (2.49) | |||
| (2.50) |
The sum of the diagonal elements of the stress tensor is zero (since the virial is zero) and the matrix is symmetric.
Lastly, it should be noted that the above description does not take into account the possible inclusion of distance-dependent 1-4 interactions, as permitted by some force fields. Such interactions are permissible in DL_POLY_2 and are described in the section on pair potentials below. DL_POLY_2 also permits scaling of the 1-4 interactions by a numerical factor. 1-4 interactions do, of course, contribute to the atomic virial.
In DL_POLY_2 dihedral forces are handled by the routine DIHFRC.
![]()