DL_POLY_2 also allows atomic sites to be tethered to a fixed point in space,
![]() taken as their
position at the beginning of the simulation. This is also known as position restraining.
The specification, which comes as part of the molecular description,
requires a tether potential type and the associated interaction parameters.
taken as their
position at the beginning of the simulation. This is also known as position restraining.
The specification, which comes as part of the molecular description,
requires a tether potential type and the associated interaction parameters.
Note, firstly, that application of tethering potentials means that momentum will no longer be a conserved quantity of the simulation. Secondly, in constant pressure simulations, where the MD cell changes size or shape, the reference position is scaled with the cell vectors.
The potential functions available in DL_POLY_2 are as
follows, in each case ![]() is the distance of the atom from its position at
is the distance of the atom from its position at ![]() :
:
| (2.63) |
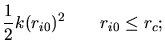 |
(2.64) | ||
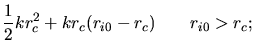 |
(2.65) |
| (2.66) |
The force on the atom ![]() arising from a tether potential is obtained
using the general formula:
arising from a tether potential is obtained
using the general formula:
| (2.67) |
The contribution to be added to the atomic virial is given by
| (2.68) |
The contribution to be added to the atomic stress tensor is
given by
| (2.69) |
In DL_POLY_2 bond forces are handled by the routine TETHFRC.