![]()
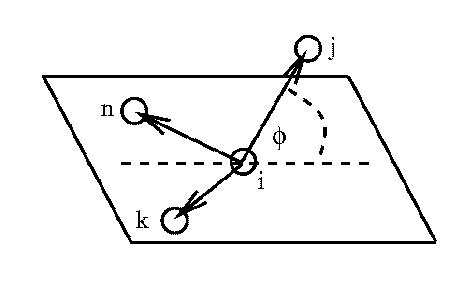
The inversion angle and associated vectors
The inversion angle potentials describe the interaction arising from a particular geometry of three atoms around a central atom. The best known example of this is the arrangement of hydrogen atoms around nitrogen in ammonia to form a trigonal pyramid. The hydrogens can `flip' like an inverting umbrella to an alternative structure, which in this case is identical, but in principle causes a change in chirality. The force restraining the ammonia to one structure can be described as an inversion potential (though it is usually augmented by valence angle potentials also). The inversion angle is defined in the figure above - note that the inversion angle potential is a sum of the three possible inversion angle terms. It resembles a dihedral potential in that it requires the specification of four atomic positions.
The potential functions available in DL_POLY_2 are as follows.
| (2.51) |
| (2.52) |
| (2.53) |
In these formulae ![]() is the inversion angle defined by
is the inversion angle defined by
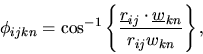 |
(2.54) |
with
| (2.55) |
and the unit vectors
| (2.56) |
As usual, ![]() etc. and the hat
etc. and the hat ![]() indicates a unit vector in
the direction of
indicates a unit vector in
the direction of ![]() . The total inversion potential requires
the calculation of three such angles, the formula being derived from the above using the
cyclic permutation of the indices
. The total inversion potential requires
the calculation of three such angles, the formula being derived from the above using the
cyclic permutation of the indices ![]() etc.
etc.
Equivalently, the angle ![]() may be written as
may be written as
![\begin{displaymath}
\phi_{ijkn}=\cos^{-1} \left \{ \frac{
[(\mbox{$\underline{r}...
...mbox{$\underline{\hat{v}}$}_{kn})^{2}]^{1/2}}{r_{ij}}\right \}
\end{displaymath}](img195.png) |
(2.57) |
Formally, the force on an atom arising from the inversion potential
is given by
| (2.58) |
with ![]() being one of
being one of ![]() and
and ![]() one of
one of ![]() . This may be expanded into
. This may be expanded into
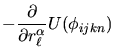 |
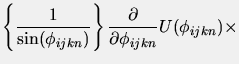 |
||
![$\displaystyle \frac{\partial}{\partial r_{\ell}^{\alpha}}
\left\{\frac{[(\mbox{...
...r}$}_{ij}\cdot\mbox{$\underline{\hat{v}}$}_{kn})^{2}]^{1/2}}
{r_{ij}}\right \}.$](img198.png) |
(2.59) |
Following through the (extremely tedious!) differentiation gives the result:
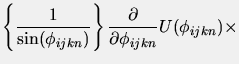 |
(2.60) | ||
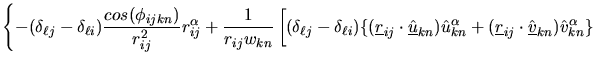 |
|||
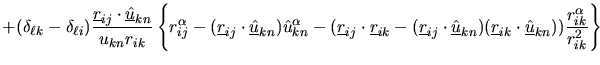 |
|||
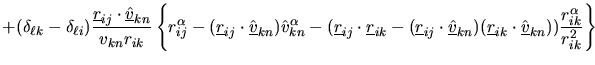 |
|||
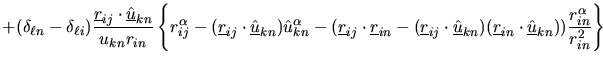 |
|||
![$\displaystyle \left . \left .+ (\delta_{\ell n}-\delta_{\ell i})
\frac{\mbox{$\...
...hat{v}}$}_{kn}))\frac{r_{in}^{\alpha}}{r_{in}^{2}}
\right \} \right ] \right \}$](img204.png) |
This general formula applies to all atoms ![]() . It must be remembered however, that
these formulae apply to just one of the three contributing terms (i.e. one angle
. It must be remembered however, that
these formulae apply to just one of the three contributing terms (i.e. one angle ![]() ) of the
full inversion potential: specifically the inversion
angle pertaining to the out-of-plane vector
) of the
full inversion potential: specifically the inversion
angle pertaining to the out-of-plane vector ![]() . The contributions
arising from the other vectors
. The contributions
arising from the other vectors ![]() and
and ![]() are
obtained by the cyclic permutation of the indices in the manner described above. All these
force contributions must be added to the final atomic forces.
are
obtained by the cyclic permutation of the indices in the manner described above. All these
force contributions must be added to the final atomic forces.
Formally, the contribution to be added to the atomic virial is given by
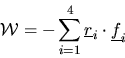 |
(2.61) |
However it is possible to show by thermodynamic arguments (cf [26],) or simply from the fact that the sum of forces on atoms j,k and n is equal and opposite to the force on atom i, that the inversion potential makes no contribution to the atomic virial.
If the force components ![]() for atoms
for atoms ![]() are calculated using the
above formulae, it is easily seen that the contribution to be added to the atomic stress
tensor is given by
are calculated using the
above formulae, it is easily seen that the contribution to be added to the atomic stress
tensor is given by
| (2.62) |
The sum of the diagonal elements of the stress tensor is zero (since the virial is zero) and the matrix is symmetric.
In DL_POLY_2 inversion forces are handled by the routine INVFRC.
![]()