



Next: Metal Potentials
Up: The Intermolecular Potential Functions
Previous: The Intermolecular Potential Functions
Contents
Index
Short Ranged (van der Waals) Potentials
The short ranged pair forces available in DL_POLY_2 are as
follows.
- 12 - 6 potential: (12-6)
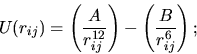 |
(2.70) |
- Lennard-Jones: (lj)
![\begin{displaymath}
U(r_{ij})=4\epsilon\left[\left
(\frac{\sigma}{r_{ij}}\right)^{12}-\left(\frac{\sigma}{r_{ij}}\right)^{6}\right
];
\end{displaymath}](img221.png) |
(2.71) |
- n - m potential [27]: (nm)
![\begin{displaymath}
U(r_{ij})=\frac{E_{o}}{(n-m)}\left[m\left
(\frac{r_{o}}{r_{ij}}\right)^{n}-n\left(\frac{r_{o}}{r_{ij}}\right)^{m}\right
];
\end{displaymath}](img222.png) |
(2.72) |
- Buckingham potential: (buck)
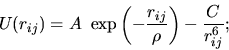 |
(2.73) |
- Born-Huggins-Meyer potential: (bhm)
![\begin{displaymath}
U(r_{ij})=A~\exp[B(\sigma-r_{ij})]-\frac{C}{r_{ij}^{6}}-\frac{D}{r_{ij}^{8}};
\end{displaymath}](img224.png) |
(2.74) |
- Hydrogen-bond (12 - 10) potential: (hbnd)
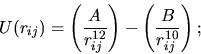 |
(2.75) |
- Shifted force n - m potential [27]: (snm)
with
This peculiar form has the advantage over the standard shifted n-m
potential in that both 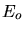 and
and 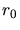 (well depth and location of
minimum) retain their original values after the shifting process.
(well depth and location of
minimum) retain their original values after the shifting process.
- Morse potential: (mors)
![\begin{displaymath}
U(r_{ij})=E_{o}[\{1-\exp(-k(r_{ij}-r_{o}))\}^{2}-1];
\end{displaymath}](img79.png) |
(2.80) |
- Tabulation: (tab). The potential is defined numerically only.
The parameters defining these potentials are supplied to
DL_POLY_2 at run time (see the description of the FIELD file in section
4.1.3). Each atom type in the system is specified by a unique
eight-character label defined by the user. The pair potential is then
defined internally by the combination of two atom labels.
As well as the numerical parameters defining the potentials,
DL_POLY_2 must also be provided with a cutoff radius 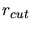 ,
which sets a range limit on the computation of the interaction.
Together with the parameters, the cutoff is used by the subroutine
FORGEN (or FORGEN/SMALL>_RSQ) to construct an interpolation
array vvv for the potential function over the range 0 to
,
which sets a range limit on the computation of the interaction.
Together with the parameters, the cutoff is used by the subroutine
FORGEN (or FORGEN/SMALL>_RSQ) to construct an interpolation
array vvv for the potential function over the range 0 to
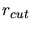 . A second array ggg is also calculated, which is
related to the potential via the formula:
. A second array ggg is also calculated, which is
related to the potential via the formula:
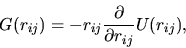 |
(2.81) |
and is used in the calculation of the forces. Both arrays are
tabulated in units of energy. The use of interpolation arrays, rather
than the explicit formulae, makes the routines for calculating the
potential energy and atomic forces very general, and
enables the use of user defined pair potential functions.
DL_POLY_2 also allows the user to read in the interpolation arrays
directly from a file (see the description of the FORTAB routine
(chapter 8) and the TABLE file (section 4.1.5).
This is particularly useful
if the pair potential function has no simple analytical description
(e.g. spline potentials).
The force on an atom  derived from one of these potentials is
formally calculated with the standard formula:
derived from one of these potentials is
formally calculated with the standard formula:
![\begin{displaymath}
\mbox{$\underline{f}$}_{j}=-\frac{1}{r_{ij}}\left[\frac{\par...
...{\partial
r_{ij}}U(r_{ij})\right]\mbox{$\underline{r}$}_{ij},
\end{displaymath}](img237.png) |
(2.82) |
where
 . The force on atom
. The force on atom  is
the negative of this.
is
the negative of this.
The contribution to be added to the atomic virial (for each pair
interaction) is
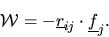 |
(2.83) |
The contribution to be added to the atomic stress tensor is
given by
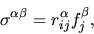 |
(2.84) |
where 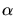 and
and 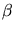 indicate the
indicate the 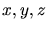 components. The atomic
stress tensor derived from the pair forces is symmetric.
components. The atomic
stress tensor derived from the pair forces is symmetric.
Since the calculation of pair potentials assumes a spherical cutoff
(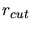 ) it is necessary to apply a long range
correction to
the system potential energy and virial. Explicit formulae are needed
for each case and are derived as follows. For two atom types
) it is necessary to apply a long range
correction to
the system potential energy and virial. Explicit formulae are needed
for each case and are derived as follows. For two atom types 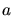 and
and
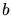 , the correction for the potential energy is calculated via the
integral
, the correction for the potential energy is calculated via the
integral
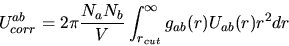 |
(2.85) |
where 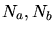 are the numbers of atoms of types
are the numbers of atoms of types 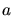 and
and 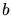 ,
, 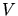 is the system volume and
is the system volume and 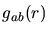 and
and 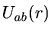 are the
appropriate pair correlation function and pair potential respectively.
It is usual to assume
are the
appropriate pair correlation function and pair potential respectively.
It is usual to assume 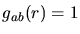 for
for 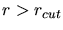 . DL_POLY_2
sometimes makes the additional assumption that the repulsive part of
the short ranged potential is negligible beyond
. DL_POLY_2
sometimes makes the additional assumption that the repulsive part of
the short ranged potential is negligible beyond 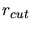 .
.
The correction for the system virial is
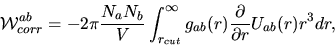 |
(2.86) |
where the same approximations are applied. Note that these formulae
are based on the assumption that the system is reasonably isotropic
beyond the cutoff.
In DL_POLY_2 the short ranged forces are calculated by one of the
routines SRFRCE, SRFRCE/SMALL>_RSQ, and SRFRCENEU. The long
range corrections are calculated by routine LRCORRECT. The
calculation makes use of the Verlet neighbour list described above.




Next: Metal Potentials
Up: The Intermolecular Potential Functions
Previous: The Intermolecular Potential Functions
Contents
Index
W Smith
2003-05-12
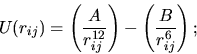
![\begin{displaymath}
U(r_{ij})=4\epsilon\left[\left
(\frac{\sigma}{r_{ij}}\right)^{12}-\left(\frac{\sigma}{r_{ij}}\right)^{6}\right
];
\end{displaymath}](img221.png)
![\begin{displaymath}
U(r_{ij})=\frac{E_{o}}{(n-m)}\left[m\left
(\frac{r_{o}}{r_{ij}}\right)^{n}-n\left(\frac{r_{o}}{r_{ij}}\right)^{m}\right
];
\end{displaymath}](img222.png)
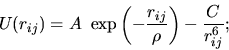
![\begin{displaymath}
U(r_{ij})=A~\exp[B(\sigma-r_{ij})]-\frac{C}{r_{ij}^{6}}-\frac{D}{r_{ij}^{8}};
\end{displaymath}](img224.png)
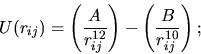
![$\displaystyle \frac{\alpha E_{o}}{(n-m)}\left [
m\beta^{n}\left \{ \left (\frac...
...r_{o}}{r_{ij}}\right )^{m}-
\left(\frac{1}{\gamma}\right)^{m}\right \} \right ]$](img226.png)
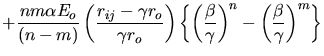
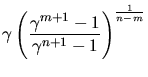
![$\displaystyle \frac{(n-m)}{[n\beta^{m}(1+(m/\gamma-m-1)/\gamma^{m})-
m\beta^{n}(1+(n/\gamma-n-1)/\gamma^{n})]}$](img233.png)
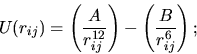
![\begin{displaymath}
U(r_{ij})=4\epsilon\left[\left
(\frac{\sigma}{r_{ij}}\right)^{12}-\left(\frac{\sigma}{r_{ij}}\right)^{6}\right
];
\end{displaymath}](img221.png)
![\begin{displaymath}
U(r_{ij})=\frac{E_{o}}{(n-m)}\left[m\left
(\frac{r_{o}}{r_{ij}}\right)^{n}-n\left(\frac{r_{o}}{r_{ij}}\right)^{m}\right
];
\end{displaymath}](img222.png)
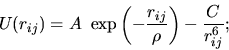
![\begin{displaymath}
U(r_{ij})=A~\exp[B(\sigma-r_{ij})]-\frac{C}{r_{ij}^{6}}-\frac{D}{r_{ij}^{8}};
\end{displaymath}](img224.png)
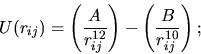
![$\displaystyle \frac{\alpha E_{o}}{(n-m)}\left [
m\beta^{n}\left \{ \left (\frac...
...r_{o}}{r_{ij}}\right )^{m}-
\left(\frac{1}{\gamma}\right)^{m}\right \} \right ]$](img226.png)
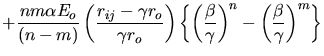
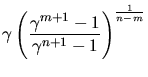
![$\displaystyle \frac{(n-m)}{[n\beta^{m}(1+(m/\gamma-m-1)/\gamma^{m})-
m\beta^{n}(1+(n/\gamma-n-1)/\gamma^{n})]}$](img233.png)
![]() ,
which sets a range limit on the computation of the interaction.
Together with the parameters, the cutoff is used by the subroutine
FORGEN (or FORGEN/SMALL>_RSQ) to construct an interpolation
array vvv for the potential function over the range 0 to
,
which sets a range limit on the computation of the interaction.
Together with the parameters, the cutoff is used by the subroutine
FORGEN (or FORGEN/SMALL>_RSQ) to construct an interpolation
array vvv for the potential function over the range 0 to
![]() . A second array ggg is also calculated, which is
related to the potential via the formula:
. A second array ggg is also calculated, which is
related to the potential via the formula:
![]()
![]() derived from one of these potentials is
formally calculated with the standard formula:
derived from one of these potentials is
formally calculated with the standard formula:
![\begin{displaymath}
\mbox{$\underline{f}$}_{j}=-\frac{1}{r_{ij}}\left[\frac{\par...
...{\partial
r_{ij}}U(r_{ij})\right]\mbox{$\underline{r}$}_{ij},
\end{displaymath}](img237.png)
![]() ) it is necessary to apply a long range
correction to
the system potential energy and virial. Explicit formulae are needed
for each case and are derived as follows. For two atom types
) it is necessary to apply a long range
correction to
the system potential energy and virial. Explicit formulae are needed
for each case and are derived as follows. For two atom types ![]() and
and
![]() , the correction for the potential energy is calculated via the
integral
, the correction for the potential energy is calculated via the
integral