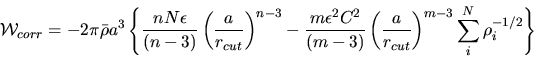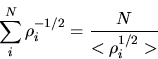



Next: Three Body Potentials
Up: The Intermolecular Potential Functions
Previous: Short Ranged (van der
Contents
Index
Metal Potentials
DL_POLY_2 includes density dependent potentials suitable for
calculating the properties of metals. The basic model is due to
Finnis and Sinclair [28] as implemented by Sutton and
Chen
[7]. The form of the potential is: (stch)
![\begin{displaymath}
U_{sc}=\epsilon\left[\sum_{i<j}\left(\frac{a}{r_{ij}}\right )^{n}
-C\sum_{i}\rho_{i}^{1/2}\right ],
\end{displaymath}](img249.png) |
(2.87) |
where the local density 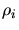 is given by
is given by
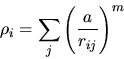 |
(2.88) |
The Sutton-Chen potential has the advantage that it is decomposable
into pair contributions and thus falls within the general tabulation
scheme of DL_POLY_2 , where it is treated as a short ranged
interaction. The same form of potential may be used in alloys, through
the appropriate choice of parameters 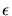 and
and 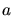 . The
parameters
. The
parameters 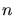 and
and 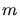 however must be the same for all component
elements. DL_POLY_2 calculates this potential in two stages: the first
calculates the local density
however must be the same for all component
elements. DL_POLY_2 calculates this potential in two stages: the first
calculates the local density 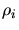 for each atom; and the second
calculates the potential energy and forces. Interpolation arrays are
used in both these stages.
for each atom; and the second
calculates the potential energy and forces. Interpolation arrays are
used in both these stages.
The total force
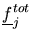 on an atom
on an atom 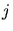 derived from this
potential is calculated in the standard way:
derived from this
potential is calculated in the standard way:
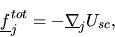 |
(2.89) |
which gives
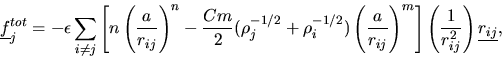 |
(2.90) |
which is recognisable as a sum of pair forces, for example the force
on atom 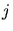 due to the atom
due to the atom 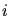 :
:
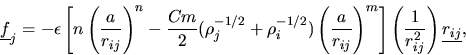 |
(2.91) |
where
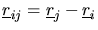 . The force on atom
. The force on atom 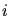 is
the negative of this.
is
the negative of this.
With the pair forces thus defined the contribution to be added to the
atomic virial from each atom pair is then
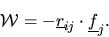 |
(2.92) |
The contribution to be added to the atomic stress tensor is
given by
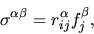 |
(2.93) |
where 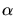 and
and 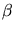 indicate the
indicate the 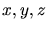 components. The atomic
stress tensor is symmetric.
components. The atomic
stress tensor is symmetric.
The long range correction for the system potential is in two parts.
Firstly by analogy with the short ranged potentials
the correction to the local density is obtained by
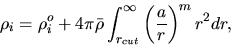 |
(2.94) |
where 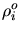 is the uncorrected local density and
is the uncorrected local density and 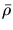 is the mean particle density. Evaluating the integral yields
is the mean particle density. Evaluating the integral yields
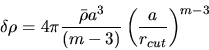 |
(2.95) |
which is the local density correction and is identical for all atoms.
The correction is applied immediately after the local
density is calculated. The density term of the Sutton Chen potential
needs no further correction. The pair term correction is obtained by
analogy with the short ranged potentials and is
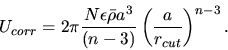 |
(2.96) |
The correction to the local density having already been applied.
To estimate the virial correction we assume the corrected local
densities are constants (i.e. independent of distance - at least
beyond the range 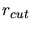 ). This allows the virial correction to be
computed by the methods used in the short ranged potentials. The result is:
). This allows the virial correction to be
computed by the methods used in the short ranged potentials. The result is:
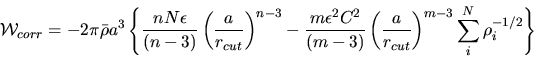 |
(2.97) |
This correction may be used as it stands, or with the further
approximation:
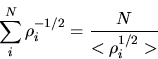 |
(2.98) |
where
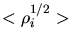 is regarded as a constant of the system.
is regarded as a constant of the system.
In DL_POLY_2 the metal forces are handled by the routine SUTTCHEN. The local density is calculated by routines SCDENS
and DENLOC. The long range corrections are calculated by LRCMETAL.

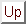



Next: Three Body Potentials
Up: The Intermolecular Potential Functions
Previous: Short Ranged (van der
Contents
Index
W Smith
2003-05-12
![\begin{displaymath}
U_{sc}=\epsilon\left[\sum_{i<j}\left(\frac{a}{r_{ij}}\right )^{n}
-C\sum_{i}\rho_{i}^{1/2}\right ],
\end{displaymath}](img249.png)
![\begin{displaymath}
U_{sc}=\epsilon\left[\sum_{i<j}\left(\frac{a}{r_{ij}}\right )^{n}
-C\sum_{i}\rho_{i}^{1/2}\right ],
\end{displaymath}](img249.png)
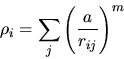
![]() on an atom
on an atom ![]() derived from this
potential is calculated in the standard way:
derived from this
potential is calculated in the standard way:
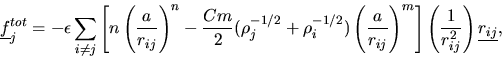
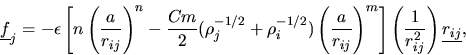
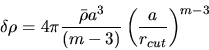
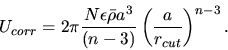
![]() ). This allows the virial correction to be
computed by the methods used in the short ranged potentials. The result is:
). This allows the virial correction to be
computed by the methods used in the short ranged potentials. The result is: