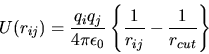 |
(2.118) |
This form of the Coulomb sum has the advantage that it drastically reduces the range of electrostatic interactions, without giving rise to a violent step in the potential energy at the cutoff. Its main use is for preliminary preparation of systems and it is not recommended for realistic models.
The form of the potential function is
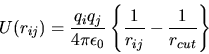 |
(2.118) |
The force on an atom ![]() derived from this potential, within the radius
derived from this potential, within the radius
![]() , is
, is
| (2.119) |
The contribution to the atomic virial is
| (2.120) |
The contribution to be added to the atomic stress tensor is
given by
| (2.121) |
In DL_POLY_2 these forces are handled by the routine COUL1.
A further refinement of this approach is to truncate the ![]() potential
at
potential
at ![]() and add a linear term to the potential in order to make
both the energy and the force zero at the cutoff. The potential is thus
and add a linear term to the potential in order to make
both the energy and the force zero at the cutoff. The potential is thus
![\begin{displaymath}
U(r_{ij}) = {q_i q_j \over 4\pi\epsilon_0} \left[ {1\over r_...
... +
{r_{ij}\over r_{\rm cut}^2} - {2\over r_{\rm cut}} \right]
\end{displaymath}](img288.png) |
(2.122) |
![\begin{displaymath}
\mbox{$\underline{f}$}_{j}=\frac{q_{i}q_{j}}{4\pi\epsilon_{0...
...} - {1\over r_{\rm cut}^2} \right]
\mbox{$\underline{r}$}_{ij}
\end{displaymath}](img289.png) |
(2.123) |
This removes the heating effects that arise from the discontinuity in the forces at the cutoff in the simple truncated and shifted potential. The physics of this potential however are little better. It is only recommended for very crude structure optimizations.
The contribution to the atomic virial is
| (2.124) |
The contribution to be added to the atomic stress tensor is
given by
| (2.125) |
In DL_POLY_2 these forces are handled by the routine COUL4.