Direct Coulomb Sum

Use of the direct Coulomb sum is sometimes necessary for accurate simulation of isolated (nonperiodic) systems. It is not recommended for periodic systems.

The interaction potential for two charged ions is

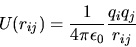$$U(r_{ij})=\frac{1}{4\pi\epsilon_{0}}\frac{q_{i}q_{j}}{r_{ij}}$$ (2.114)

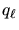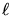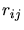with $q_{\ell}$ the charge on an atom labelled $\ell$, and $r_{ij}$ the magnitude of the separation vector $\mbox{$\underline{r}$}_{ij}=\mbox{$\underline{r}$}_{j}-\mbox{$\underline{r}$}_{i}$.

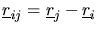The force on an atom 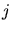$j$ derived from this force is

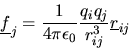$$\mbox{$\underline{f}$}_{j}=\frac{1}{4\pi\epsilon_{0}}\frac{q_{i}q_{j}}{r_{ij}^{3}}\mbox{$\underline{r}$}_{ij}$$ (2.115)

with the force on atom 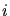$i$ the negative of this.

The contribution to the atomic virial is

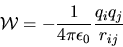$${\cal W}=-\frac{1}{4\pi\epsilon_{0}}\frac{q_{i}q_{j}}{r_{ij}}$$ (2.116)

which is simply the negative of the potential term.

The contribution to be added to the atomic stress tensor is

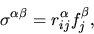$$\sigma^{\alpha \beta}=r_{ij}^{\alpha}f_{j}^{\beta},$$ (2.117)

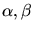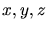where $\alpha,\beta$ are $x,y,z$ components. The atomic stress tensor is symmetric.

In DL_POLY_2 these forces are handled by the routines COUL0 and COUL0NEU.