



Next: Dynamical Shell Model
Up: Long Ranged Electrostatic (Coulombic)
Previous: Hautman Klein Ewald (HKE)
Contents
Index
Reaction Field
In the reaction field method it is assumed that
any given molecule is surrounded by a spherical cavity of finite
radius within which the electrostatic interactions are calculated
explicitly. Outside the cavity the system is treated as a
dielectric continuum. The
occurence of any net dipole within the cavity induces a polarisation
in the dielectric, which in turn interacts with the given
molecule. The model allows the replacement of the infinite Coulomb sum
by a finite sum plus the reaction field.
The reaction field model coded into DL_POLY_2 is the implementation of
Neumann based on charge-charge interactions [33]. In
this model, the total Coulombic potential is given by
![\begin{displaymath}
U_{c}=\frac{1}{4\pi\epsilon_{0}}\sum_{j<n}q_{j}q_{n}
\left [ \frac{1}{r_{nj}}+\frac{B_{0}r_{nj}^{2}}{2 R_{c}^{3}} \right ]
\end{displaymath}](img421.png) |
(2.163) |
where the second term on the right is the reaction field correction to
the explicit sum, with 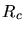 the radius of the cavity. The constant
the radius of the cavity. The constant
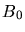 is defined as
is defined as
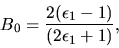 |
(2.164) |
with 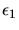 the dielectric constant outside the cavity.
The effective pair potential is therefore
the dielectric constant outside the cavity.
The effective pair potential is therefore
![\begin{displaymath}
U(r_{nj})=\frac{1}{4\pi\epsilon_{0}} q_{j}q_{n}
\left [ \frac{1}{r_{nj}}+\frac{B_{0}r_{nj}^{2}}{2 R_{c}^{3}} \right ].
\end{displaymath}](img426.png) |
(2.165) |
This expression unfortunately leads to large fluctuations in the system
Coulombic energy, due to the large `step' in the function at the
cavity boundary. In DL_POLY_2 this is countered by subtracting the value of
the potential at the cavity boundary from each pair contribution. The
term subtracted is
![\begin{displaymath}
\frac{1}{4\pi\epsilon_{0}} \frac{q_{j}q_{n}}{R_{c}}
\left [ 1+\frac{B_{0}}{2} \right ].
\end{displaymath}](img427.png) |
(2.166) |
The effective pair force on an atom 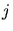 arising from another atom
arising from another atom 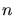 within the cavity is given by
within the cavity is given by
![\begin{displaymath}
\mbox{$\underline{f}$}_{j}=\frac{q_{j}q_{n}}{4\pi\epsilon_{0...
...}}-\frac{B_{0}}{R_{c}^{3}}\right ]\mbox{$\underline{r}$}_{nj}.
\end{displaymath}](img428.png) |
(2.167) |
The contribution of each effective pair interaction to the atomic
virial is
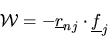 |
(2.168) |
and the contribution to the atomic stress tensor is
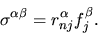 |
(2.169) |
In DL_POLY_2 the reaction field is handled by the routines COUL3 and COUL3NEU.




Next: Dynamical Shell Model
Up: Long Ranged Electrostatic (Coulombic)
Previous: Hautman Klein Ewald (HKE)
Contents
Index
W Smith
2003-05-12
![\begin{displaymath}
U_{c}=\frac{1}{4\pi\epsilon_{0}}\sum_{j<n}q_{j}q_{n}
\left [ \frac{1}{r_{nj}}+\frac{B_{0}r_{nj}^{2}}{2 R_{c}^{3}} \right ]
\end{displaymath}](img421.png)
![\begin{displaymath}
U_{c}=\frac{1}{4\pi\epsilon_{0}}\sum_{j<n}q_{j}q_{n}
\left [ \frac{1}{r_{nj}}+\frac{B_{0}r_{nj}^{2}}{2 R_{c}^{3}} \right ]
\end{displaymath}](img421.png)
![\begin{displaymath}
U(r_{nj})=\frac{1}{4\pi\epsilon_{0}} q_{j}q_{n}
\left [ \frac{1}{r_{nj}}+\frac{B_{0}r_{nj}^{2}}{2 R_{c}^{3}} \right ].
\end{displaymath}](img426.png)
![]() arising from another atom
arising from another atom ![]() within the cavity is given by
within the cavity is given by
![\begin{displaymath}
\mbox{$\underline{f}$}_{j}=\frac{q_{j}q_{n}}{4\pi\epsilon_{0...
...}}-\frac{B_{0}}{R_{c}^{3}}\right ]\mbox{$\underline{r}$}_{nj}.
\end{displaymath}](img428.png)