



Next: Berendsen Barostat
Up: Barostats
Previous: Barostats
Contents
Index
The Hoover Barostat
DL_POLY_2 uses the Melchionna modification of the Hoover algorithm
[38] in which the equations of motion involve
a Nosé - Hoover thermostat and a barostat in the same spirit.
Cell size variation
For isotropic fluctuations the equations of motion are:
where 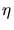 is the barostat friction coefficient,
is the barostat friction coefficient, 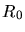 the system
centre of mass,
the system
centre of mass, 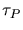 a specified time constant for pressure
fluctuations,
a specified time constant for pressure
fluctuations, 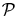 the instantaneous pressure and
the instantaneous pressure and 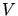 the system
volume.
the system
volume.
The conserved quantity is, to within a constant, the Gibbs free energy
of the system:
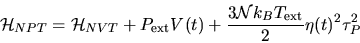 |
(2.191) |
The algorithm is readily implemented in the leapfrog scheme:
Like the Nosé-Hoover thermostat, several iterations are required to
obtain self consistency. DL_POLY_2 uses 4 iterations (5 if bond constraints
are present) with the standard Verlet leapfrog predictions for the
initial estimates of 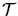 ,
, 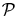 ,
,
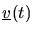 and
and
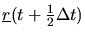 . Note also that the change in box
size requires the SHAKE algorithm to be called each iteration with the
new cell vectors obtained from:
. Note also that the change in box
size requires the SHAKE algorithm to be called each iteration with the
new cell vectors obtained from:
where
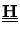 is the cell matrix whose columns are the three cell vectors
is the cell matrix whose columns are the three cell vectors
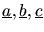 .
.
The isotropic changes to cell volume are implemented in the DL_POLY
routine NPT_H1 which allows for systems containing bond
constraints.
Cell size and shape variation
The isotropic algorithm may be extended to allowing the cell shape to
vary by defining 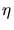 as a tensor,
as a tensor,
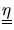 . The equations of
motion are implemented as:
. The equations of
motion are implemented as:
where
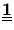 is the identity matrix and
is the identity matrix and
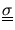 the pressure tensor. The new cell vectors are calculated from
the pressure tensor. The new cell vectors are calculated from
DL_POLY_2 uses a power series expansion truncated at the quadratic term to
approximate the exponential of the tensorial term. The new volume is
found from
![\begin{displaymath}
V(t+\Delta t) \leftarrow V(t) \exp\left[ \Delta t\; {\rm tr}(\mbox{$\underline{\underline{\bf\eta}}$})\right]
\end{displaymath}](img543.png) |
(2.196) |
The conserved quantity is
![\begin{displaymath}
{\cal H}_{NPT} = {\cal H}_{NVT} + P_{\rm ext} V(t) + {3 {\ca...
...m tr}
[\mbox{$\underline{\underline{\bf\eta}}$}(t)]^2 \tau_P^2
\end{displaymath}](img544.png) |
(2.197) |
This algorithm is implemented in the routines NST_H0 (nonbonded
systems) and NST_H1 (with bond constraints).




Next: Berendsen Barostat
Up: Barostats
Previous: Barostats
Contents
Index
W Smith
2003-05-12
![$\displaystyle {\mbox{$\underline{f}$}(t)\over m} - \left[\chi(t)+\eta(t)\right]\mbox{$\underline{v}$}(t)$](img509.png)
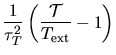
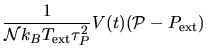
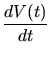
![$\displaystyle {\mbox{$\underline{f}$}(t)\over m} - \left[\chi(t)+\eta(t)\right]\mbox{$\underline{v}$}(t)$](img509.png)
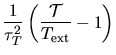
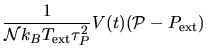
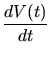
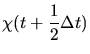
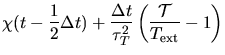
![$\displaystyle {1\over 2} \left[\chi(t-{1\over 2}\Delta t)+\chi(t+{1\over 2}\Delta t)\right]$](img488.png)
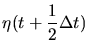
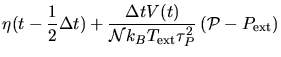
![$\displaystyle {1\over 2} \left[\eta(t-{1\over 2}\Delta t)+\eta(t+{1\over 2}\Delta t)\right]$](img524.png)
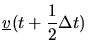
![$\displaystyle \mbox{$\underline{v}$}(t-{1\over 2} \Delta t) +
\Delta t\left[ {\...
...{f}$}(t)\over m} - \left[\chi(t)+\eta(t)\right]\mbox{$\underline{v}$}(t)\right]$](img525.png)
![$\displaystyle {1\over 2} \left[\mbox{$\underline{v}$}(t-{1\over 2}\Delta t)
+\mbox{$\underline{v}$}(t+{1\over 2}\Delta t)\right]$](img491.png)
![$\displaystyle \mbox{$\underline{r}$}(t) + \Delta t \left(\mbox{$\underline{v}$}...
...x{$\underline{r}$}(t+{1\over 2}\Delta t)-\mbox{$\underline{R}$}_0\right]\right)$](img526.png)
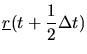
![$\displaystyle {1\over 2} \left[ \mbox{$\underline{r}$}(t)+ \mbox{$\underline{r}$}(t+\Delta t)\right]$](img528.png)
![$\displaystyle V(t) \exp\left[3\Delta t\; \eta(t+{1\over 2}\Delta t)\right]$](img531.png)
![$\displaystyle \mbox{$\underline{\underline{\bf H}}$}(t)\exp\left[\Delta t \;\eta(t+{1\over 2}\Delta t)\right]$](img533.png)
![]() as a tensor,
as a tensor,
![]() . The equations of
motion are implemented as:
. The equations of
motion are implemented as:
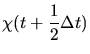
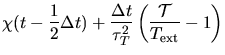
![$\displaystyle {1\over 2} \left[\chi(t-{1\over 2}\Delta t)+\chi(t+{1\over 2}\Delta t)\right]$](img488.png)
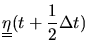
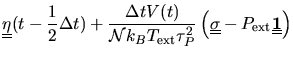
![$\displaystyle {1\over 2} \left[\mbox{$\underline{\underline{\bf\eta}}$}(t-{1\ov...
...Delta t)+
\mbox{$\underline{\underline{\bf\eta}}$}(t+{1\over 2}\Delta t)\right]$](img539.png)
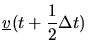
![$\displaystyle \mbox{$\underline{v}$}(t-{1\over 2} \Delta t) +
\Delta t\left[ {\...
...ox{$\underline{\underline{\bf\eta}}$}(t)\right]\mbox{$\underline{v}$}(t)\right]$](img540.png)
![$\displaystyle {1\over 2} \left[\mbox{$\underline{v}$}(t-{1\over 2}\Delta t)
+\mbox{$\underline{v}$}(t+{1\over 2}\Delta t)\right]$](img491.png)
![$\displaystyle \mbox{$\underline{r}$}(t) + \Delta t \left(\mbox{$\underline{v}$}...
...x{$\underline{r}$}(t+{1\over 2}\Delta t)-\mbox{$\underline{R}$}_0\right]\right)$](img526.png)
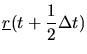
![$\displaystyle {1\over 2} \left[ \mbox{$\underline{r}$}(t)+ \mbox{$\underline{r}$}(t+\Delta t)\right]$](img528.png)
![$\displaystyle \mbox{$\underline{\underline{\bf H}}$}(t)\exp\left[\Delta t \;\mbox{$\underline{\underline{\bf\eta}}$}(t+{1\over 2}\Delta t)\right]$](img542.png)