Contents   Index

Distributing the Nonbonded Terms

In DL_POLY_2 the nonbonded interactions are handled with a Verlet neighbour list [12] which is reconstructed at intervals during the simulation. This list records the indices of all `secondary' atoms within a certain radius of each `primary' atom; the radius being the cut-off radius ($r_{cut}$) normally applied to the nonbonded potential function, plus an additional increment ( $\Delta r_{cut}$). The larger radius ( $r_{cut}+\Delta r_{cut}$) permits the same list to be used for several timesteps without requiring an update. The frequency at which the list must be updated clearly depends on the thickness of the region $\Delta r_{cut}$. In RD, the neighbour list is constructed simultaneously on each node and in such a way as to share the total burden of the work equally between nodes. Each node is responsible for a unique set of nonbonded interactions and the neighbour list is therefore different on each node. DL_POLY_2 uses a method based on the Brode-Ahlrichs scheme [22] (see figure below) to construct the neighbour list.

Additional modifications are necessary to handle the excluded atoms [43]. A distributed excluded atoms list is constructed by DL_POLY_2 at the start of the simulation. The list is constructed so that the excluded atoms are referenced in the same order as they would appear in the Verlet neighbour list if the bonded interactions were ignored, allowing for the distributed structure of the neighbour list.

 

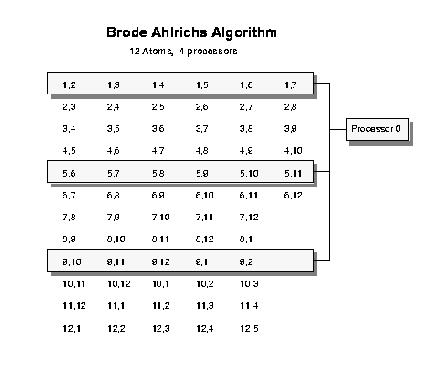
Schematic diagram of the parallel implementation of the Brode-Ahlrichs algorithm.

The diagram illustrates the reordering of the upper triangular matrix of n(n-1)/2 pair interactions so that the rows of the matrix are of approximately equally length. Each entry in the table consists of a primary atom index (constant within a row) and a ``neighbouring'' atom index. Rows are assigned sequentially to nodes. In the diagram node 0 deals with rows 1, 5 and 9, node 1 to rows 2, 6, and 10 etc.

When a charge group scheme (as opposed to an atomistic scheme) is used for the non-bonded terms, the group-group interactions are distributed using the Brode-Ahlrichs approach. This makes the Verlet list considerably smaller, thus saving memory, but also results in a more ``coarse grain'' parallelism. The consequence of which is that performance with a large number of processors will degrade more quickly than with the atomistic scheme.

Once the neighbour list has been constructed, each node of the parallel computer may proceed independently to calculate the pair force contributions to the atomic forces.

  Contents   Index