Contents   Index

Smoothed Particle Mesh Ewald

As its name implies the Smoothed Particle Mesh Ewald (SPME) method is a modification of the standard Ewald method. DL_POLY_2 implements the SPME method of Essmann et al. [31]. Formally this method is capable of treating van der Waals forces also, but in DL_POLY_2 it is confined to electrostatic forces only. The main difference from the standard Ewald method is in its treatment of the the reciprocal space terms. By means of an interpolation procedure involving (complex) B-splines, the sum in reciprocal space is represented on a three dimensional rectangular grid. In this form the Fast Fourier Transform (FFT) may be used to perform the primary mathematical operation, which is a 3D convolution. The efficiency of these procedures greatly reduces the cost of the reciprocal space sum when the range of $\mbox{$\underline{k}$}$ vectors is large. The method (briefly) is as follows (for full details see [31]):

1. Interpolation of the $exp(-i\mbox{$\underline{k}$}\cdot\mbox{$\underline{r}$}_{j})$ terms (given here for one dimension):
   

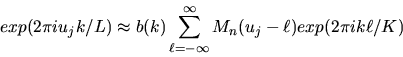   $$exp(2\pi i u_{j}k/L) \approx b(k) \sum_{\ell=-\infty}^{\infty} M_{n}(u_{j}-\ell) exp(2\pi i k\ell/K)$$ (2.139)

   
   

   in which $k$ is the integer index of the $\mbox{$\underline{k}$}$ vector in a principal direction, $K$ is the total number of grid points in the same direction and $u_{j}$ is the fractional coordinate of ion $j$ scaled by a factor $K$ (i.e. $u_{j}=K s_{j}^{x}$). Note that the definition of the B-splines implies a dependence on the integer $K$, which limits the formally infinite sum over $\ell$. The coefficients $M_{n}(u)$ are B-splines of order $n$ and the factor $b(k)$ is a constant computable from the formula:
   

   $$b(k)=exp(2\pi i (n-1)k/K)\left [\sum_{\ell=0}^{n-2} M_{n}(\ell+1) exp(2\pi i k\ell/K)\right ]^{-1}$$ (2.140)

   
   
2. Approximation of the structure factor $S(\mbox{$\underline{k}$})$:
   

   $$S(\mbox{$\underline{k}$}) \approx b_{1}(k_{1}) b_{2}(k_{2}) b_{3}(k_{3}) Q^{\dagger}(k_{1},k_{2},k_{3})$$ (2.141)

   
   

   where $Q^{\dagger}(k_{1},k_{2},k_{3})$ is the discrete Fourier transform of the charge array $Q(\ell_{1},\ell_{2},\ell_{3})$ defined as
   

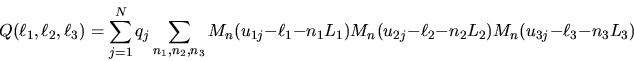   $$Q(\ell_{1},\ell_{2},\ell_{3})=\sum_{j=1}^{N}q_{j}\sum_{n_{1}... ...(u_{2j}-\ell_{2}-n_{2}L_{2}) M_{n}(u_{3j}-\ell_{3}-n_{3}L_{3})$$ (2.142)

   
   

   (in which the sums over $n_{1,2,3}$ etc are required to capture contributions from all relevant periodic cell images, which in practice means the nearest images.)

3. Approximating the reciprocal space energy $U_{recip}$:
   

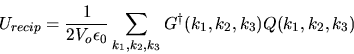   $$U_{recip}=\frac{1}{2V_{o}\epsilon_{0}}\sum_{k_{1},k_{2},k_{3}} G^{\dagger}(k_{1},k_{2},k_{3})Q(k_{1},k_{2},k_{3})$$ (2.143)

   
   

   in which $G^{\dagger}$ is the discrete Fourier transform of the function
   

   $$G(k_{1},k_{2},k_{3})= \frac{\exp(-k^{2}/4\alpha^{2})}{k^{2}} B(k_{1},k_{2},k_{3}) (Q^{\dagger}(k_{1},k_{2},k_{3}))^{*}$$ (2.144)

   
   

   and where
   

   $$B(k_{1},k_{2},k_{3})=\vert b_{1}(k_{1})\vert^{2} \vert b_{2}(k_{2})\vert^{2} \vert b_{3}(k_{3})\vert^{2}$$ (2.145)

   
   

   and $(Q^{\dagger}(k_{1},k_{2},k_{3}))^{*}$ is the complex conjgate of $Q^{\dagger}(k_{1},k_{2},k_{3})$. The function $G(k_{1},k_{2},k_{3})$ is thus a relatively simple product of the gaussian screening term appearing in the conventional Ewald sum, the function $B(k_{1},k_{2},k_{3})$ and the discrete Fourier transform of $Q(k_{1},k_{2},k_{3})$

4. Calculating the atomic forces, which are given formally by:
   

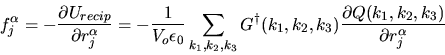   $$f_{j}^{\alpha}=-\frac{\partial U_{recip}}{\partial r_{j}^{\a... ... \frac{\partial Q(k_{1},k_{2},k_{3})}{\partial r_{j}^{\alpha}}$$ (2.146)

   
   

Fortunately, due to the recursive properties of the B-splines, these formulae are easily evaluated.

The virial and the stress tensor are calculated in the same manner as for the conventional Ewald sum.

The DL_POLY_2 subroutines required to calculate the SPME contributions are:
BSPGEN, which calculates the B-splines; BSPCOE, which calculates B-spline coefficients; SPL_CEXP, which calculates the FFT and B-spline complex exponentials; EWALD_SPME, which calculates the reciprocal space contributions; SPME_FOR, which calculates the reciprocal space forces; and DLPFFT3, which calculates the 3D complex fast Fourier transform (default code only, Cray, SGI, IBM SP machines have their own FFT routines, selected at compile time and the FFTW public FFT is also an option). These subroutines calculate the reciprocal space components of the Ewald sum only, the real-space calculations are performed by EWALD2, EWALD3 and EWALD 4, as for the normal Ewald sum. In addition there are a few minor utility routines : CPY_RTC copies a real array to a complex array; ELE_PRD is an element-for-element product of two arrays; SCL_CSUM is a scalar sum of elements of a complex array; and SET_BLOCK initialises an array to a present value (usually zero).

  Contents   Index