Berendsen Thermostat

In the Berendsen algorithm the instantaneous temperature is pushed towards the desired temperature by scaling the velocities at each step:

$\displaystyle \chi$	$\textstyle \leftarrow$	$\displaystyle \left[ 1+ {\Delta t\over \tau_T}\left({T_{\rm ext}\over {\cal T}}-1\right) \right]^{1/2}$
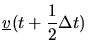$\displaystyle \mbox{$\underline{v}$}(t + {1\over 2} \Delta t)$	$\textstyle \leftarrow$	$\displaystyle \left[ \mbox{$\underline{v}$}(t-{1\over 2} \Delta t) + \Delta t {\mbox{$\underline{f}$}(t)\over m}\right]\chi$
$\displaystyle \mbox{$\underline{v}$}(t)$	$\textstyle \leftarrow$	$\displaystyle {1\over 2} \left[\mbox{$\underline{v}$}(t-{1\over 2}\Delta t) +\mbox{$\underline{v}$}(t+{1\over 2}\Delta t)\right]$
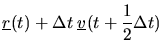$\displaystyle \mbox{$\underline{r}$}(t+\Delta t)$	$\textstyle \leftarrow$	$\displaystyle \mbox{$\underline{r}$}(t) + \Delta t \; \mbox{$\underline{v}$}(t+{1\over 2}\Delta t)$	(2.185)

As with the Nosé-Hoover thermostat iteration is required to obtain self consistency of $\chi$ , $\mbox{$\underline{v}$}(t)$ and ${\cal T}$ , although it should be noted $\chi$ has different roles in the two thermostats. The Berendsen algorithm conserves total momentum but not energy.

As with the Nosé-Hoover algorithm the presence of constraint bonds requires an additional iteration with one application of SHAKE corrections. The algorithm is implemented in the DL_POLY routines NVT_B0 and NVT_B1, the latter being for systems with bond constraints.