Contents   Index

Gaussian Constraints

Kinetic temperature can be made a constant of the equations of motion by imposing an additional constraint on the system. If one writes the equations of motions as :

$${d \mbox{$\underline{r}$}(t) \over d t} = \mbox{$\underline{v}$}(t)$$

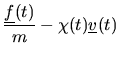$${d \mbox{$\underline{v}$}(t) \over d t} = {\mbox{$\underline{f}$}(t)\over m} - \chi(t) \mbox{$\underline{v}$}(t)$$ (2.186)

with the temperature constraint

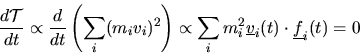$${d{\cal T}\over dt} \propto {d \over dt}\left(\sum_i (m_i v_... ...mbox{$\underline{v}$}_i(t)\cdot\mbox{$\underline{f}$}_i(t) = 0$$ (2.187)

then choosing

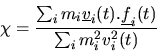$$\chi = {\sum_i m_i \mbox{$\underline{v}$}_i(t).\mbox{$\underline{f}$}_i(t) \over \sum_i m_i^2 v_i^2(t)}$$ (2.188)

minimizes the ``least squares'' differences between the Newtonian and constrained trajectories. Following Brown and Clarke [37] the algorithm is implemented by calculating $\eta = 1/(1+ \chi\Delta t/2)$

$$\eta \leftarrow \sqrt{{T_{\rm ext}\over {\cal T}}}$$

$$\mbox{$\underline{v}$}(t + {1\over 2} \Delta t) \leftarrow (2\eta-1) \mbox{$\underline{v}$}(t-{1\over2}\Delta t) + \eta\Delta t {\mbox{$\underline{f}$}(t)\over m}$$

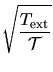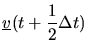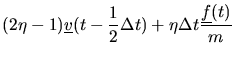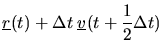$$\mbox{$\underline{r}$}(t+\Delta t) \leftarrow \mbox{$\underline{r}$}(t) + \Delta t \; \mbox{$\underline{v}$}(t+{1\over 2}\Delta t)$$ (2.189)

where ${\cal T}$ is obtained from standard Verlet leapfrog integration. Only one iteration is needed (two if the system has bond constraints) to constrain the instantaneous temperature to exactly $T_{\rm ext}$ however energy is not conserved by this algorithm.

The algorithm is implemented in the DL_POLY routines NVT_E0 and NVT_E1. The latter is for systems with bond constraints.

  Contents   Index