



Next: The DL_POLY_2 Multiple Timestep
Up: Rigid Bodies and Rotational
Previous: Integration of the Rigid
Contents
Index
The above integration algorithm can be used for rigid bodies in a
system containing ``atomic'' species (whose equations of motion are
integrated with the standard leapfrog algorithm). These rigid bodies
may even be linked to other species (including other rigid bodies) by
extensible bonds. However if a rigid body is linked to an atom or
another rigid body by a bond constraint the above algorithm is
not adequate. The reason is that the constraint will introduce an
additional force and torque onto the body that can only be found after the integration of the unconstrained unit. DL_POLY_2 has a suite of
integration algorithms to cope with this situation in which both the
constraint conditions and the quaternion equations are solved
similtaneously using an extension of the SHAKE algorithm called
``QSHAKE'' [15].
The QSHAKE algorithm proceeds as follows: Consider the figure in which
two rigid bodies are linked by a constraint bond. We seek to choose
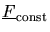 so that at the end of the integration step the
two sites in the constraint bond are a distance
so that at the end of the integration step the
two sites in the constraint bond are a distance 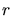 apart. The
integration of the bodies as free units leaves the sites
apart. The
integration of the bodies as free units leaves the sites 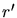 apart. Since the constraint force produces both a force and torque on
the rigid units the correction to the constrained sites position must
include both the translation and rotation of the body as a whole. The
translational contribution is
apart. Since the constraint force produces both a force and torque on
the rigid units the correction to the constrained sites position must
include both the translation and rotation of the body as a whole. The
translational contribution is
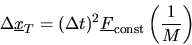 |
(2.215) |
The torque induced by the constraint force is
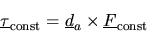 |
(2.216) |
so the correction to the angular velocity of the body is
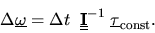 |
(2.217) |
The ``rotational'' correction to the position of the site is thus
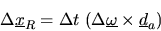 |
(2.218) |
which in general will not be in the same direction as
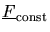 and
and
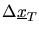 . If we denote the components of
. If we denote the components of
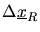 parallel and perpendicular to
parallel and perpendicular to
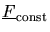 by
by
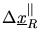 and
and
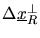 the
correction to the site position is
the
correction to the site position is
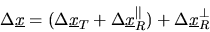 |
(2.219) |
Clearly the presence of the constraint force and torque will mean the
positions and velocities of the remaining sites in the rigid body will
also have to be corrected. We proceed by seeking an approximation to
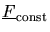 then reintegrating the rigid
body equations of motion with the improved total forces and torques on
the body. A few iterations are normally sufficient to achieve
convergence: If we assume the bond distance
then reintegrating the rigid
body equations of motion with the improved total forces and torques on
the body. A few iterations are normally sufficient to achieve
convergence: If we assume the bond distance 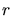 is large in comparison
to the correction then after the correction is made the bond length is
is large in comparison
to the correction then after the correction is made the bond length is
where
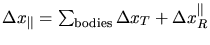 and
and
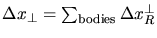 . Thus a first order correction to the position of the
constrained site is
. Thus a first order correction to the position of the
constrained site is
where
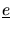 is the unit vector
is the unit vector
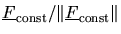 . The term in the
. The term in the  defines an effective mass,
defines an effective mass,
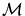 : where
: where
![$1/{\cal M} = 1/ M +
\left[ \left(\mbox{$\underline{\underline{\bf I}}$}^{-1}\le...
...ght)\right)
\times \mbox{$\underline{d}$}_a \right]\cdot \mbox{$\underline{e}$}$](img606.png) .
.
The effective reduced mass for the two linked bodies,  and
and 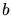 , is
, is
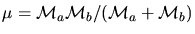 . As in the
standard SHAKE algorithm, the reduced mass can then be used to predict
the constraint force
. As in the
standard SHAKE algorithm, the reduced mass can then be used to predict
the constraint force
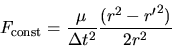 |
(2.222) |
Note that each prediction of the constraint force requires the rigid
body equations of motion to be reintegrated accurately. If two bodies
are linked by one constraint bond only two or three iterations are
necessary for convergence. However convergence may be slower if an
extended network of linked bodies is involved. Note also that the
reduced mass needs to be re-evaluated every time-step because it
depends on the relative orienation of the two bodies. Finally, we note
the algorithm reduces to the standard SHAKE algorithm if the rigid
bodies are replaced by point atoms. In such a case, even though
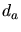 is zero, care must be taken to avoid the singularity arising
from
is zero, care must be taken to avoid the singularity arising
from
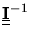 .
.
This ``linked rigid body'' algorithm is implemented in NVEQ_2
with the QSHAKE corrections to the forces applied in QSHAKE.
Again it is straightforward to couple these systems to a Hoover type
or Berendsen thermostat and/or barostat. The Hoover and Berendsen
thermostated versions are found in NVTQ_H2 and NVTQ_B2
respectively. The isotropic constant pressure implementations are
found in NPTQ_H2 and NPTQ_B2, while the anisotropic
constant pressure routines are found in NSTQ_H2 and NSTQ_B2. An outline of the parallel version of QSHAKE is given in
section 2.6.8.




Next: The DL_POLY_2 Multiple Timestep
Up: Rigid Bodies and Rotational
Previous: Integration of the Rigid
Contents
Index
W Smith
2003-05-12
![]() so that at the end of the integration step the
two sites in the constraint bond are a distance
so that at the end of the integration step the
two sites in the constraint bond are a distance ![]() apart. The
integration of the bodies as free units leaves the sites
apart. The
integration of the bodies as free units leaves the sites ![]() apart. Since the constraint force produces both a force and torque on
the rigid units the correction to the constrained sites position must
include both the translation and rotation of the body as a whole. The
translational contribution is
apart. Since the constraint force produces both a force and torque on
the rigid units the correction to the constrained sites position must
include both the translation and rotation of the body as a whole. The
translational contribution is
![$\displaystyle \surd\left[ \left(r^\prime + \Delta x_\parallel\right)^2
+ \left( \Delta x_\perp\right)^2\right]$](img593.png)
![$\displaystyle { ( \Delta t)^2 \mbox{$\underline{F}$}_{\rm const}}
\left\{ { 1\o...
...
\times \mbox{$\underline{d}$}_a \right]\cdot \mbox{$\underline{e}$} \ \right\}$](img601.png)
![]() and
and ![]() , is
, is
![]() . As in the
standard SHAKE algorithm, the reduced mass can then be used to predict
the constraint force
. As in the
standard SHAKE algorithm, the reduced mass can then be used to predict
the constraint force