Contents   Index

The DL_POLY_2 Multiple Timestep Algorithm

For simulations employing a large spherical cutoff $r_{cut}$ in the calculation of the interactions DL_POLY_2 offers the possibility of using a multiple timestep algorithm to improve the efficiency. The method is based on that described by Streett et al [39,40] with extension to Coulombic systems by Forester et al [41].

In themultiple timestep algorithm there are two cutoffs for the pair interactions: a relatively large cutoff ($r_{cut}$) which is used to define the standard Verlet neighbour list; and a smaller cutoff $r_{prim}$ which is used to define a primary list within the larger cutoff sphere (see figure). Forces derived from atoms in the primary list are generally much larger than those derived from remaining (so-called secondary) atoms in the neighbour list. Good energy conservation is therefore possible if the forces derived from the primary atoms are calculated every timstep, while those from the secondary atoms are calculated much less frequently, and are merely extrapolated over the interval. DL_POLY_2 handles this procedure as follows.

DL_POLY_2 updates the Verlet neighbour list at irregular intervals, determined by the movement of atoms in the neighbour list (see section 2.1). The interval between updates is usually of the order of $\sim$20 timesteps. Partitioning the Verlet list into primary and secondary atoms always occurs when the Verlet list is updated, and thereafter at intervals of multt timesteps (i.e. the multi-step interval specified by the user - see section 4.1.1). Immediately after the partitioning, the force contributions from both the primary and secondary atoms are calculated. The forces are again calculated in total in the subsequent timestep. Thereafter, for multt-2 timesteps, the forces derived from the primary atoms are calculated explicitly, while those derived from the secondary atoms are calculated by linear extrapolation of the exact forces obtained in the first two timesteps of the multi-step interval. It is readily apparent how this scheme can lead to a significant saving in execution time.

Extension of this basic idea to simulations using the Ewald sum requires the following:

1. the reciprocal space terms are calculated only for the first two timesteps of the multi-step,
2. the contribution to the reciprocal space terms arising from primary interactions are immediately subtracted, leaving only the long-range components. (This is done in real space, by subtracting erf terms.);
3. the real space Coulombic forces arising from the secondary atoms are calculated in the first two timesteps of the multi-step using the normal Ewald expressions (i.e. the erfc terms).
4. the Coulombic forces arising from primary atoms are calculated at every timestep in real space assuming the full Coulombic force;

In this way the Coulombic forces can be handled by the same multiple timestep scheme as the van der Waals forces. The algorithm is described in detail in [41].

Note that the accuracy of the algorithm is a function of the multi-step interval multt, and decreases as multt increases. Also, the algorithm is not time reversible and is therefore susceptible to energy drift. Its use with a thermostat is therefore advised.

 

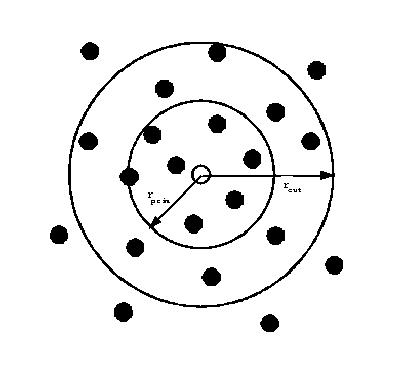
The multiple timestep algorithm

The atoms surrounding the central atom (open circle) are classified as primary if they occur within a radius $r_{prim}$ and secondary if outside this radius but within $r_{cut}$. Interactions arising from primary atoms are evaluated every timestep. Interactions from secondary atoms are calculated exactly for the first two steps of a multi-step and by extrapolation afterwards.

  Contents   Index